X
wikiHow是一个“多人协作写作系统”,因此我们的很多文章都是由多位作者共同创作的。 为了创作这篇文章,志愿作者多次对文章进行了编辑和改进。
这篇文章已经被读过114,073次。
标准差可以描述样本中的数据分布。计算标准差首先要做一些其他计算。按照这些步骤就可以快速简便地建立等式。
步骤
方法 1
方法 1 的 2:
计算方差
-
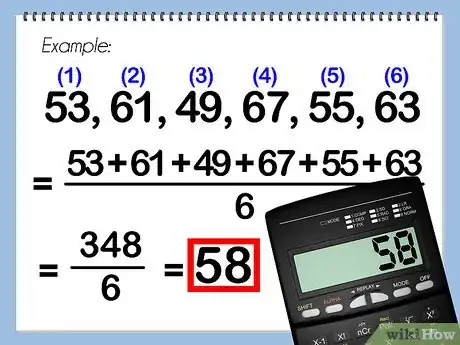
找出平均数。平均数是样本的平均值,把样本数据加起来然后除以样本数据个数就可以得到。例如:
- 样本:53, 61, 49, 67, 55, 63
- 53 + 61 + 49 + 67 + 55 + 63 = 348
- 348 / 6 = 58
- 平均数 = 58
-
找出方差。方差是数据偏离平均数的程度。得到方差首先要计算单个样本数据和平均数的差,然后平方,再求平均数。例如:
- 53 – 58 = -5; 61 – 58 = 3; 49 – 58 = -9; 67 – 58 = 9; 55 – 58 = -3; 63 – 58 = 5
- (-5)2 + 32 + (-9)2 + 92 + (-3)2 + 52 = 230
- 230 / 6 = 38.33333
- 注意,如果样本数据很大,可以除以n-1。所以这里方差可以被计算为:
- 230 / (6 – 1) = 46
-
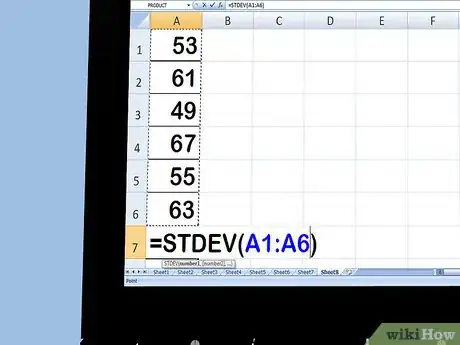
方差开方即得到标准差。标准差会告诉你数据域平均数的离散程度,约68%的样本数据在一个标准差范围内,如:
- √38.3333 = 6.19139
- 每6个数,就有4个与平均数的偏差在6.19139范围内
广告
关于本wikiHow
广告