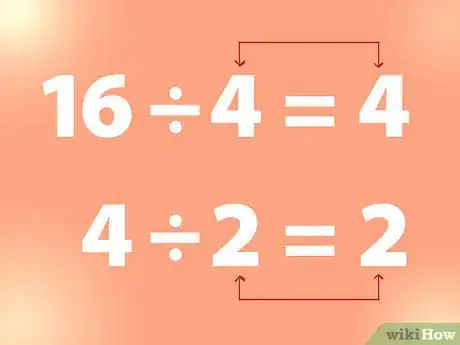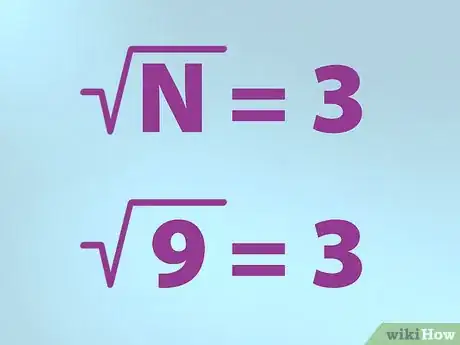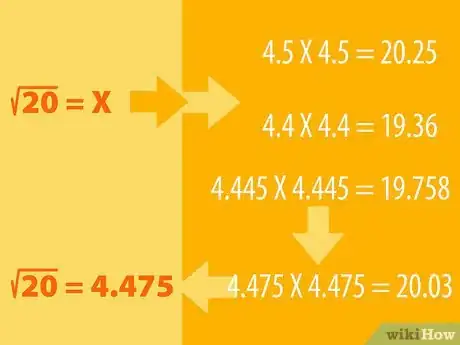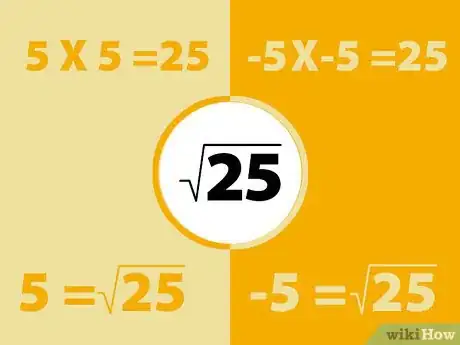X
wikiHow是一个“多人协作写作系统”,因此我们的很多文章都是由多位作者共同创作的。 为了创作这篇文章,34位用户(部分匿名)多次对文章进行了编辑和改进。
本文引用了8条参考,详情参见页面底部。
这篇文章已经被读过44,894次。
求整数的平方根很容易。但就算不是整数,有一些方法也能在不借助计算器的情况下求出任何数的平方根。当然,你需要懂得最基本的加减乘除。
步骤
方法 1
方法 1 的 3:
计算整数的平方根
-
利用乘法求平方根。求一个数的平方根会得出另一个数,后者自身相乘的积就等于前者。换种说法就是:“用哪个数自身相乘可以得出问题中的数?”
- 比如,1的平方根是1,因为1乘以1等于1(1x1=1);而4的平方根是2,因为2乘2等于4(2x2=4)。如果把平方根的概念比作一棵树,这棵树是从一粒种子长出来的。树肯定比种子大,但跟种子密切相关,种子就是它的根本。在这个例子里,4是树,2是那粒种子。
- 同理,9的平方根是3:(3X3=9),16的是4:(4X4=16),25的是5:(5X5=25),36的是6:(6X6=36),49的是7:(7X7=49),64的是8:(8X8=64),81的是9:(9X9=81),100的是10:(10X10=100)。[1]
-
利用除法求平方根。要求一个整数的平方根,也可以用整数来试除一系列的数,找到答案与除数相同的数。
- 例如:16除以4得4,4除以2得2,依此类推。在这里,4是16的平方根,2是4的平方根。
- 完全平方根没有分数或小数,因为它们都是整数。
-
使用正确的平方根符号。数学家们使用一个名叫根号的特殊符号来表示平方根。根号看起来像是一个顶上加了一条横线的对号。[2]
- N代表要求平方根的数,写在根号里面。[3]
- 如果要求9的平方根,写公式的时候就要把九(9)放在根号里面,后面写一个等号,然后写3,那意思就是9的平方根等于3。
广告
方法 2
方法 2 的 3:
求其他数的平方根
-
先假定一个答案,然后使用排除法加以验证。求非整数的平方根要难得多,但也能求出来。
- 比如说要求20的平方根。已知16是一个完全整数,其平方根是4;而25的平方根是5。那么20的平方根肯定介于这两个整数之间。
- 你可以假定20的平方根是4.5,然后直接用4.5的乘方来验算,也就是用4.5自己相乘:4.5x4.5,看结果是大于20还是小于20。如果假定的数不对,就换一个数接着试(4.6或者4.4),直到得出20。[4]
- 例如,4.5X4.5 = 20.25,逻辑上就应该尝试一个更小的数,比如4.4。而4.4X4.4 = 19.36,这样一来,20的平方根肯定就介于4.5和4.4之间。那就试试4.445X4.445 ,结果等于19.758,更接近20了。用这个方法试下去,最终就会得出4.475X4.475 = 20.03,四舍五入,就等于20。
-
使用平均法。还是要先确定出结果介于哪两个整数之间。[5]
- 然后,用要求平方根的数除以两个整数中较小一个的平方根,算出结果和较小整数平方根的平均值(也就是这两个数之和再除以2)。再用要求平方根的数除以这个平均值。最后,算出最后得出的数和第一个平均值的平均值。
- 有点绕是吗?举个例子就很清楚了。例如,10介于两个完全平方数9(3X3=9) 和16(4X4=16)之间,这两个数的平方根是3和4。那么,用10除以第一个平方根 — 3,得3.33。然后把3和 3.33相加再除以2,求出的平均数为3.1667。接下来用10除以3.1667,得3.1579。最后把3.1579和3.1667相加再除以2,得到3.1623。
- 用最后求出的数自身相乘来验算一下,在这个例子里是3.1623,3.1623乘以3.1623不就等于10.001吗?
广告
小提示
- 强烈建议记住头几个完全平方根。
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- 再记住这些:112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289...
- 还有轻松好玩的:102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, ...
广告
参考
- ↑ http://www.math.com/school/subject1/lessons/S1U1L9DP.html
- ↑ https://www.mathsisfun.com/square-root.html
- ↑ http://mathforum.org/dr.math/faq/faq.sqrt.by.hand.html
- ↑ http://www.homeschoolmath.net/teaching/square-root-algorithm.php
- ↑ http://www.factmonster.com/ipka/A0932229.html
- ↑ http://study.com/academy/lesson/finding-square-roots.html
- ↑ https://www.khanacademy.org/math/pre-algebra/exponents-radicals/radical-radicals/v/understanding-square-roots
- ↑ http://www.math.com/students/calculators/source/square-root.htm
关于本wikiHow
广告