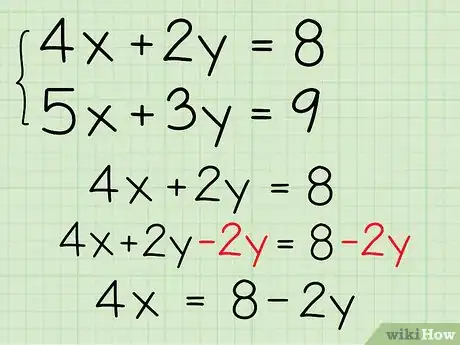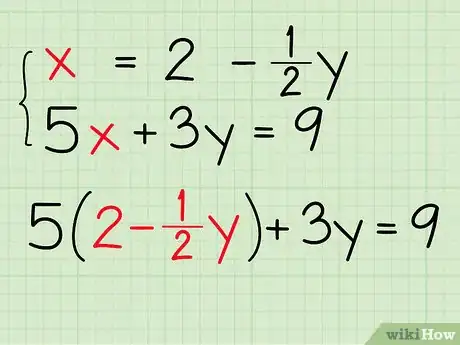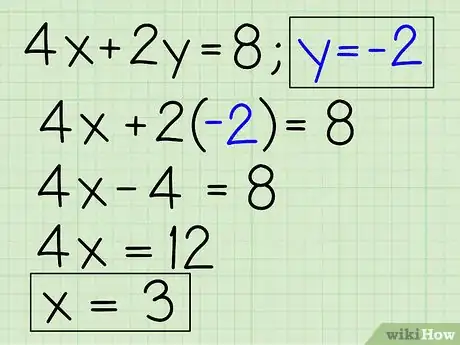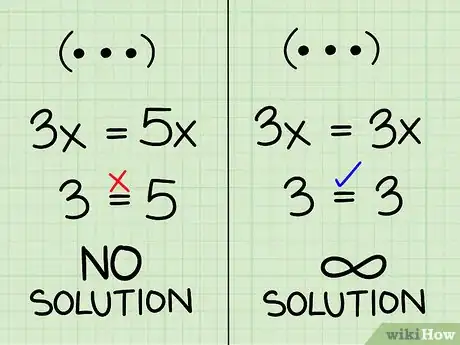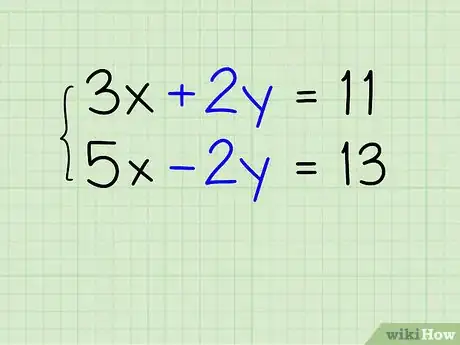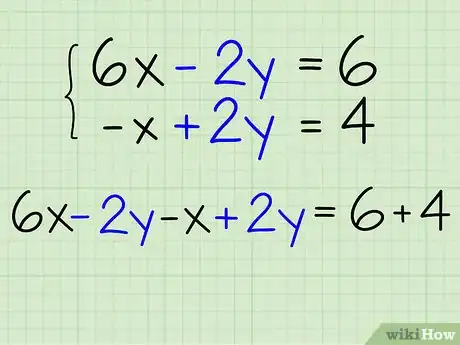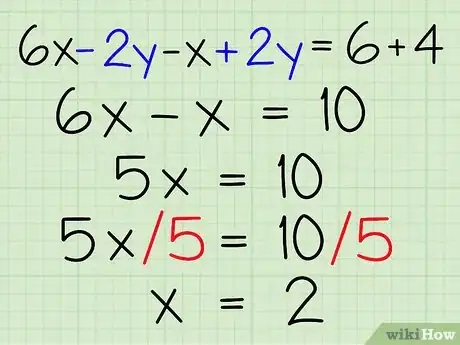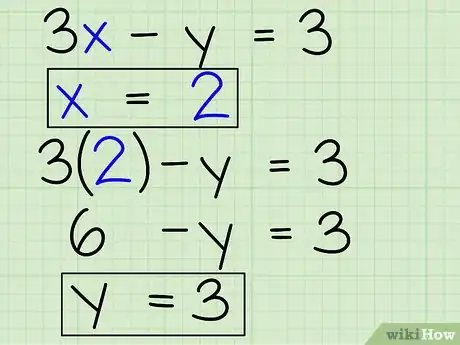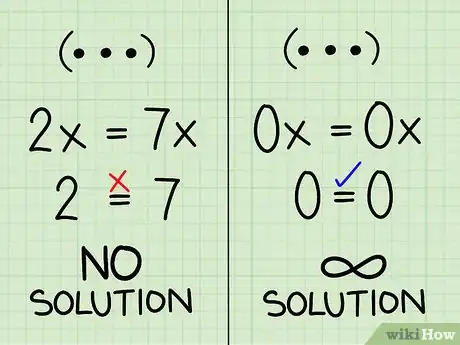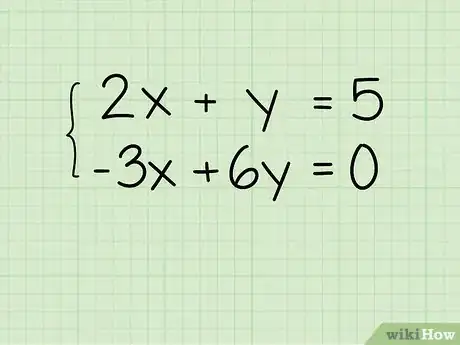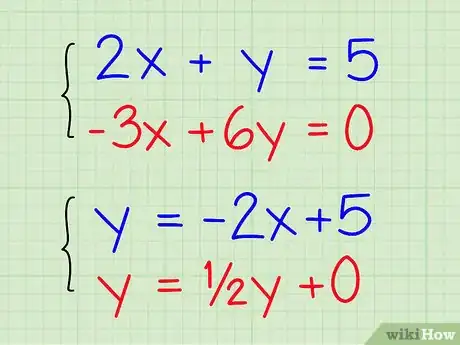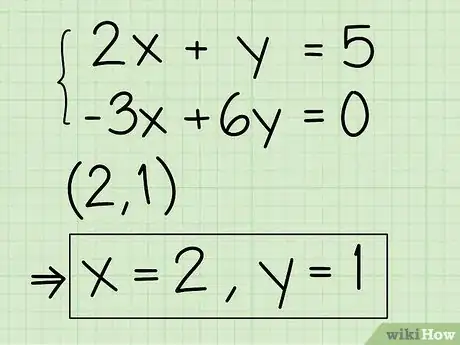X
这篇文章的共同创作者是 Grace Imson, MA. Grace Imson是一位拥有逾40年教学经验的数学老师。她目前是美国旧金山城市学院的数学老师,之前曾在圣路易斯大学的数学系就职。Grace教过小学、初中、高中和大学水平的数学。她拥有圣路易斯大学的教育文学硕士学位,专攻教育管理与监督。
这篇文章已经被读过4,288次。
“方程组”类的题目会要求你同时解出两个或两个以上的方程。当其中有两个不同的变量时,比如x和y,或a和b,乍一看,你可能会觉得题目很难。幸好,知道方法后,你只需使用基本的代数技巧,再偶尔用一点分数知识,就能解决问题。如果你是一个视觉型的学习者,或者你的老师提出要求,那么你还可以学习为方程式画图。画图对于“了解情况”或检查自己的解题过程非常有用,但是它可能比其他方法慢一点,而且不适用于所有方程组。
步骤
方法 1
方法 1 的 3:
使用代入法
-
把变量分别移到方程的两边。使用这种“代入”法时,首先你需要使用其中一个方程,“解出x”或任何其他变量。例如,假设题目中的方程为4x + 2y = 8和5x + 3y = 9。先只看第一个方程。将方程变形,两边都减去2y,得到:4x = 8 - 2y。
- 这种方法之后通常会用到分数。如果你不喜欢分数,可以尝试下文介绍的消元法。
-
方程两边同时做除法,“解出x”。当方程的一边出现x项或你使用的其他变量时,两边同时做除法,以得到变量本身。例如:
- 4x = 8 - 2y
- (4x)/4 = (8/4) - (2y/4)
- x = 2 - ½y
-
将它代入另一个方程中。一定要代入一个方程,而不是你已经用过的方程。代入已经解出的变量后,该方程就只剩下一个变量。例如:
- 已知x = 2 - ½y。
- 还没有做任何改变的第二个方程是5x + 3y = 9。
- 在第二个方程中,用”2 - ½y”代替x:5(2 - ½y) + 3y = 9。
-
解剩下的变量。现在,你得到一个只有单个变量的方程。使用普通的代数方法,解出这个变量。如果变量抵消,就跳到最后一步。在其他情况下,你会得到一个变量的解:
- 5(2 - ½y) + 3y = 9
- 10 – (5/2)y + 3y = 9
- 10 – (5/2)y + (6/2)y = 9,如果你不理解这一步的计算过程,可以去学习分数加法。这种方法经常会用到这部分知识,但并非总是如此。
- 10 + ½y = 9
- ½y = -1
- y = -2
-
使用答案去解另一个变量。不要犯解题只解一半的错误。你需要把得到的答案代入一个原始方程中,以解出另一个变量:
- 已知y = -2
- 其中一个原始方程为4x + 2y = 8。这一步可以使用两个方程中的任意一个。
- 用-2代替y:4x + 2(-2) = 8。
- 4x - 4 = 8
- 4x = 12
- x = 3
-
知道两个变量都抵消时应该怎么做。将x=3y+2或类似的答案代入另一个方程时,你想得到一个只有单个变量的方程。但是有时,你会得到一个没有变量的方程。仔细检查自己的解题过程,确保你把变形后的方程一代入到方程二中,而不是又代回到方程一。如果你确信自己没有犯任何错误,那么你的结果应该属于以下情况中的一种:[1]
- 如果你得到的方程没有变量或等式不成立,例如3 = 5,则问题无解。如果画出两个方程的图形,你会发现它们彼此平行,永不相交。
- 如果你得到一个等式成立的无变量方程,比如3 = 3,则问题有无穷多解。方程组里的两个方程是完全相等的。如果画出它们的图形,你会发现它们是同一条直线。
广告
方法 2
方法 2 的 3:
使用消元法
-
找到可以抵消的变量。有时,将两个方程相加,会恰好有一个变量可以’’抵消’’。例如,将方程3x + 2y = 11和5x - 2y = 13相加时,“+2y”和“-2y”会互相抵消,消去方程中的所有’’y’’项。观察题目中的方程,看看是否有一个变量可以像这样抵消掉。如果没有,你可以参照下一步的建议。
-
对一个方程做乘法,使得一个变量可以抵消。如果变量已经抵消,则跳过此步骤。如果两个方程中没有可以自然抵消的变量,你可以变形其中一个方程,使变量能够抵消。为了便于理解,我们来举例说明:
- 你有一个方程组:3x - y = 3和-x + 2y = 4。
- 首先,变形第一个方程,让变量y能够抵消。你也可以选择x,最后得到的答案是一样的。
- 第一个方程中的- y必须和第二个方程中的+ 2y抵消。你可以用2乘以- y,来达到这一目的。
- 用第一个方程的两边同时乘以2,2(3x - y)=2(3),得到6x - 2y = 6。这样一来,- 2y会与第二个方程中的+2y抵消。
-
把两个方程相加。两个方程相加时,用左边和左边相加,右边和右边相加。如果你使用正确的方式变形方程,其中一个变量应该会抵消。仍然以上一步中的方程组为例:
- 两个方程为6x - 2y = 6和-x + 2y = 4。
- 左侧相加得到:6x - 2y - x + 2y = ?
- 右侧相加得到:6x - 2y - x + 2y = 6 + 4。
-
解最后的变量。简化相加得到的方程,然后用基础的代数方法解最后的变量。如果简化后方程没有变量,你可以直接跳到本节的最后一步。在其他情况下,你应该可以得到其中一个变量的简单解。例如:
- 你得到6x - 2y - x + 2y = 6 + 4。
- 将x变量和y变量分类排序:6x - x - 2y + 2y = 6 + 4。
- 简化得到:5x = 10
- 解x:(5x)/5 = 10/5,所以x = 2。
-
解另一个变量。你已经求出一个变量,但题目还没有解完。将答案代入其中一个原始方程,解出另一个变量。例如:
- 已知x = 2,而其中一个原始方程为3x - y = 3。
- 用2代替x:3(2) - y = 3
- 解方程中的y:6 - y = 3
- 6 - y + y = 3 + y,所以6 = 3 + y
- 3 = y
-
知道两个变量都抵消时应该怎么做。有时,两个方程相加会得到一个毫无意义,或至少对你解题毫无帮助的方程。从头开始,仔细检查自己的解题过程,但是,如果你确信自己没有犯错,可以按照以下情况中的一种,写下答案:[2]
- 如果相加后的方程没有变量,而且等式不成立,比如2 = 7,则方程组无解。如果画出两个方程的图形,你会发现它们彼此平行,永不相交。
- 如果相加后的方程没有变量,而且等式成立,则方程组有无穷多解。两个方程实际上是一样的。如果画出它们的图形,你会发现它们是同一条直线。
广告
方法 3
方法 3 的 3:
画出方程的图形
-
只在有要求时使用这种方法。除非使用计算机或图形计算器,否则用这种方法解方程组,很多时候只能得到近似的答案。[3] 老师或数学教科书可能会要求你使用这种方法,让你熟悉如何将方程画成直线。你也可以用这种方法来检查其他方法解出的答案。
- 该方法的基本思路是画出两个方程的图形,并找到它们的交点。这个点的x值和y值就是方程组的x值和y值。
-
解出两个方程的y。让两个方程保持独立,使用代数方法,把它们变成”y = __x + __”的形式。[4] 例如:
- 第一个方程是2x + y = 5。把它变成y = -2x + 5。
- 第二个方程是-3x + 6y = 0。把它变成6y = 3x + 0,然后简化成y = ½x + 0。
- 如果两个方程相同,则两条直线会完全“重合”。你可以写方程组有无穷多解。
-
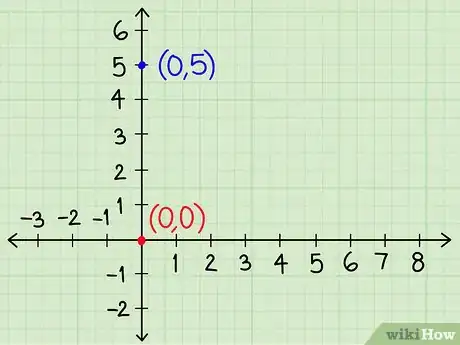
画坐标轴。在一张坐标纸上画一条垂直的“y轴”和一条水平的“x轴”。从它们的交点开始,沿y轴向上标出1、2、3、4等数字,再沿x轴向右做同样的事情。沿y轴向下、x轴向左标出-1、-2等数字。
- 如果没有坐标纸,你可以使用直尺来保证各数字之间的间距正好相等。
- 如果使用的是较大的数字或小数,你可能需要以不同的方式来调整图形比例。例如,将原本标1、2、3的点标成10、20、30或0.1、0.2、 0.3。
-
画出每条线的y轴截距。将方程变形成y = __x + __的形式后,你可以开始画出它的图形,首先画出直线与y轴相交的点。这个点在y轴上的值一定等于该方程最后面的那个数字。
- 在先前的例题中,第一条直线(y = -2x + 5)与y轴在5这个点相交。另一个方程(y = ½x + 0)的直线则在0这个点相交。它们对应的是图形中的(0,5)和(0,0)这两个点。
- 如果可以,你应该使用不同颜色的笔来画两条直线。
-
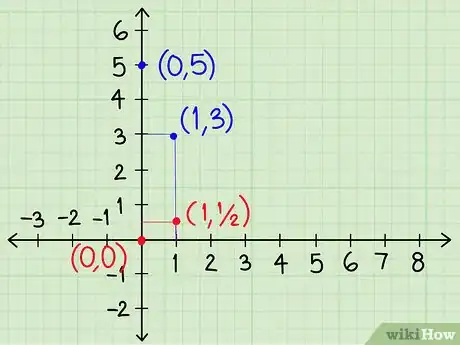
使用斜率继续画出直线。在y = __x + __形式的方程中,x前面的数字就是直线的斜率。x的值每增加1时,y值的增量等于斜率。利用这一规律,在图形中画出x=1时,两条直线上的点。你也可以把x = 1代入两个方程中,求出y的值。
- 在本例题中,直线y = -2x + 5的斜率为-2。当x = 1时,直线会从x = 0的位置向下移动2个单位。画出(0,5)和(1,3)之间的线段。
- 直线y = ½x + 0的斜率是½。当x = 1时,直线会从x = 0的位置向上移动½个单位。画出(0,0)和(1,½)之间的线段。
- 如果两条直线有相同的斜率,那么它们会永不相交,所以方程组无解。你可以写下无解二字。
-
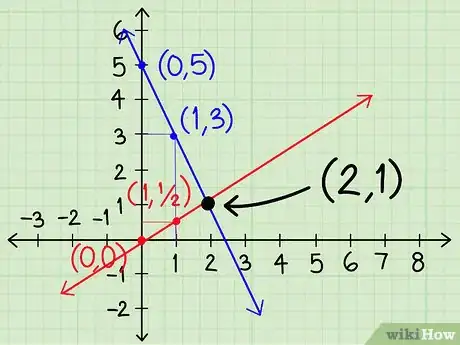
延长两条直线,直至它们相交。停下来观察图形。如果两条直线已经相交,则跳到下一步。否则,你应该根据直线的情况作出决定:
- 如果两条直线互相靠拢,那么你应该继续在这个方向上画更多的点。
- 如果两条直线彼此相距越来越远,那么你应该从x = -1开始,朝另一边画更多的点。
- 如果两条直线相距较远,试着往前画出更远的点,比如x = 10那一点。
-
在交点找到答案。两条直线相交后,交点的x值和y值就是题目的答案。在比较幸运的情况下,答案会是整数。例如,本例题中,两条直线在点(2,1)相交,所以答案是x = 2和y = 1。在某些方程组中,直线相交的值在两个整数之间,这时,除非图形非常精确,否则你很难判断它的具体位置。这种情况下,你可以直接写下答案,比如“x在1到2之间”,或使用代入法或消元法来求出准确的答案。广告
小提示
- 你可以把答案代回到原始方程中,检查自己解题过程是否正确。如果代入后,方程等式成立,比如3 = 3,则答案正确。
- 使用消元法时,为了消除变量,有时你需要用负数乘以其中一个方程。
广告
警告
- 这些方法不适用于二次或二次以上的方程,比如包含x2的方程。想了解更多关于这类方程的信息,你可以参阅二元二次方程因式分解方面的文章。[5]
广告
参考
- ↑ http://tutorial.math.lamar.edu/Classes/Alg/SystemsTwoVrble.aspx
- ↑ http://tutorial.math.lamar.edu/Classes/Alg/SystemsTwoVrble.aspx
- ↑ http://www.purplemath.com/modules/systlin2.htm
- ↑ http://www.virtualnerd.com/algebra-2/linear-systems/graphing/solve-by-graphing/equations-solution-by-graphing
- ↑ https://www.khanacademy.org/math/algebra/multiplying-factoring-expression/factoring-quadratics-in-two-vari/v/factoring-quadratics-with-two-variables
关于本wikiHow
广告