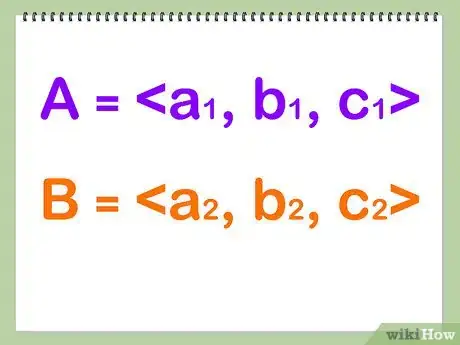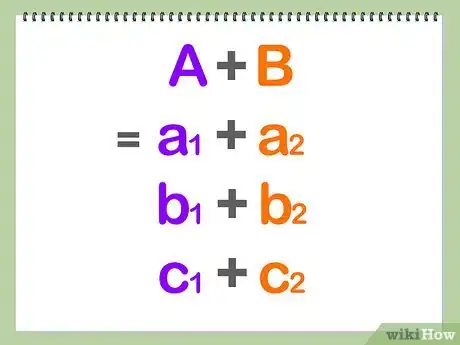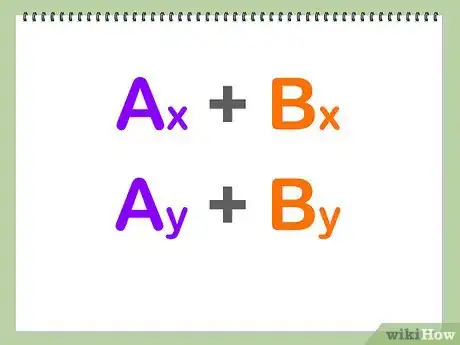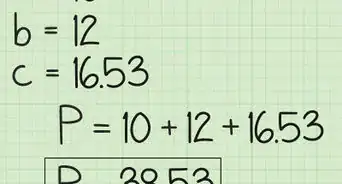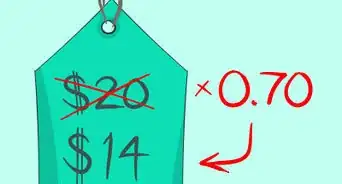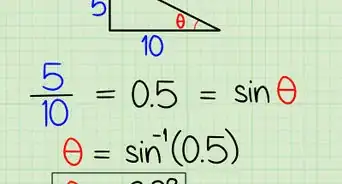如何计算向量加减法

向量是包括大小和方向的物理量，比如，速度、加速度和位移，与速率、距离、能量等只含有大小的标量不同，标量可以直接相加（比如5kj的功加6kj的功等于11kj的功），而向量的加减法要更复杂。本文将教会你如何进行向量加减法。

方法 1

方法 1 的 4:

向量加减的步骤

1
假设有两个向量，向量A和向量B，
- A=<a1,b1,c1>
- B=<a2,b2,c2>
2
如果我们想计算向量A和向量B的和，那么
- A+B = <a1+a2,b1+b2,c1+c2>
3
如果我们想从向量A中减去向量B，那么
- A-B = <a1-a2,b1-b2,c1-c2>
广告

方法 2

方法 2 的 4:

头尾相接的向量

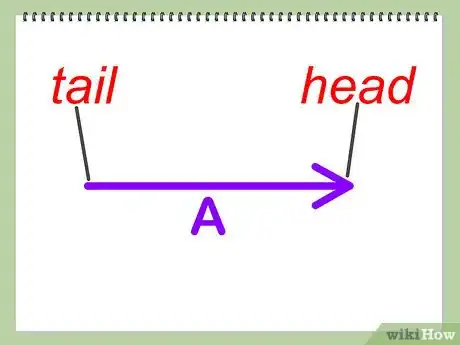
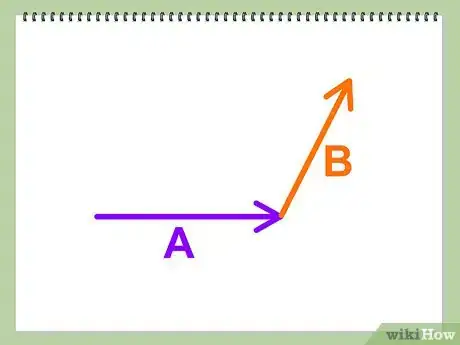
随便画一个向量，按比例缩放或者任意画一个向量都可以。如果你是按比例缩放画向量的话，一定要注意角度要保持不变。
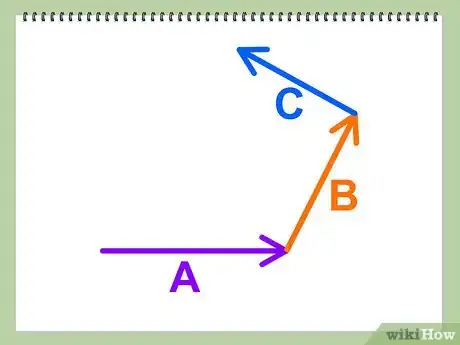
画向量的顺序以及向量的长度任意，只需要保持头尾相连即可。
4
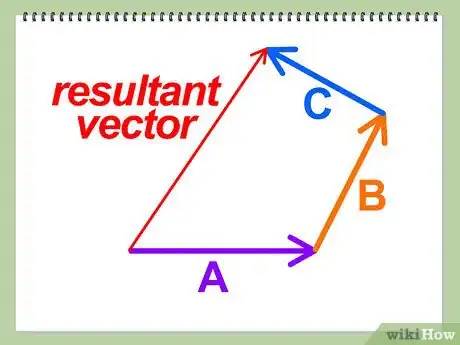
将第一个向量的尾部和最后一个向量的头部连接起来。这样就得到了一个新的向量，这个向量就是之前几个向量的合向量。
- 如果你是按照比例缩放画向量，那么你要保证角度不变，然后用尺子量出合向量的长度，再测量出合向量和指定向量的角度，或者和水平方向的夹角。
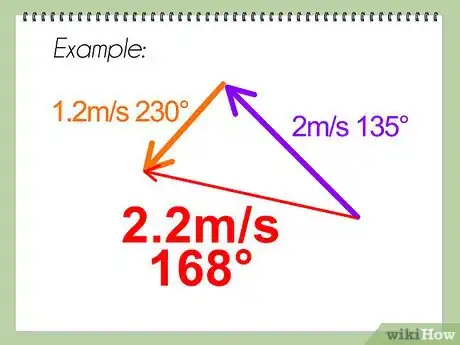
- 如果你画的是草图，你可以用三角法来计算合向量的大小。需要用到正弦定理和余弦定理。如果你要计算两个以上的向量的和，你可以先计算其中两个向量的和，然后用这两个向量的合向量再和第三个向量求和，然后以此类推。
比如，如果向量代表的是速度，那么最后的结果可以描述成，“速度是x ms^-1，和水平/垂直方向的角度是y”^o

广告

方法 3

方法 3 的 4:

向量分解

这个方法通常用在位于直角平面中的向量上，不过也可以用在别的向量上。

1
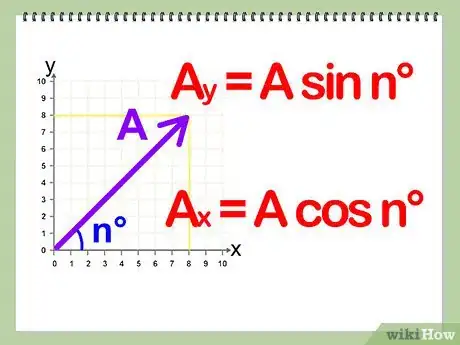
将每一个向量分解成互相垂直的两个向量。比如，将向量按照水平和垂直两个方向分解。通常在直角平面中，按照x轴方向和y轴方向分解。沿着x轴方向分解所得的向量记为i，沿着y轴方向分解所得的向量为j。
- 要将力进行分解，你需要知道力与水平方向和竖直方向，即x轴和y轴的夹角。角度已知的情况下，你可以以力作为斜边构造直接三角形，而直角三角形的两边分别沿x轴和y轴方向。两直角边的长度就是力沿这两个方向分解之后的大小，可以通过三角函数计算出来。与夹角相邻的直角边用xcos(角度)来计算，与夹角相对的直接边用xsin(角度)来计算，其中x的大小就是原力的大小。
- 如果一个分力指向左或者指向下，就给这个分力标个负号(-)。
如果某一向量前有负号(-)，那么这个向量要被减去，而不是加上。
勾股定理的形式是：c²=a²+b²，其中c代表合力的大小，a是x轴分向量大小的和，b是y轴分向量大小的和。
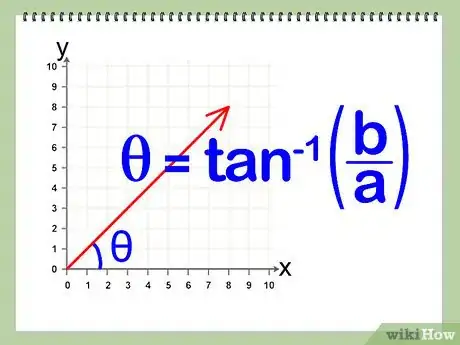
利用公式θ=tan^-1(b/a)，其中θ是合向量和水平方向的夹角。
5
描述合向量。
- 比如，如果向量代表的是力，那么结果可以描述成"大小为x N的力，与水平方向/x轴的夹角是y^o "。
广告

方法 4

方法 4 的 4:

向量减法

用一个向量减去另一个向量，可以看做是加上一个“负向量”。
负向量的大小和原向量一样，但是方向相反。你可以先画出原向量，然后在另一端标出箭头，即原向量的头变成负向量的尾，原向量的尾变成负向量的头。
用上文提到的方法，求出负向量和其余向量的合向量。

广告

小提示

不要混淆向量和标量。
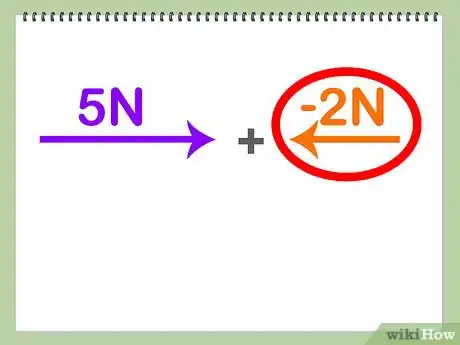
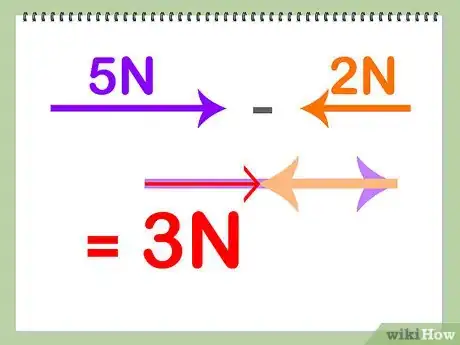
相同方向的向量可以直接对向量大小进行加减。如果你要计算两个方向相反向量的和，那么你要用其中一个向量的长度减去另一个向量的长度。
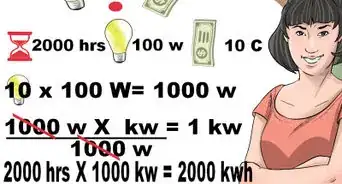
在三维空间中利用公式a²=b²+c²+d²求向量的长度。其中a是向量的大小，而b, c, d是向量在三个方向上的分量大小。
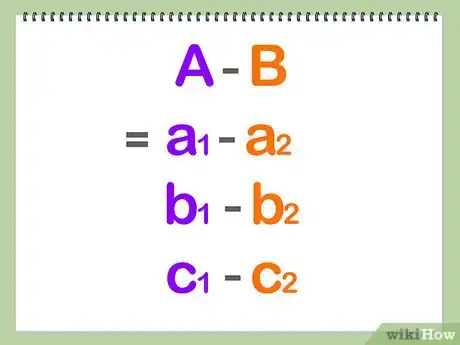
求用xi + yj + zk描述的向量之间的加减，可以直接对三个分量的系数进行加减计算。最终结果的形式同样用i,j,k来表示。
列向量之间的加减法可以直接计算每一列上数字的和或差。

广告

你可能还喜欢

广告

关于本wikiHow

wikiHow是一个“多人协作写作系统”，因此我们的很多文章都是由多位作者共同创作的。为了创作这篇文章，27位用户（部分匿名）多次对文章进行了编辑和改进。这篇文章已经被读过59,733次。

分类: 教育与交流

广告